트리 기본 용어 정리
트리는 계층 구조를 표현하는 대표적인 비선형 자료구조다. 하나의 루트 노드를 시작으로 자식 노드들이 트리 형태로 연결되어 있으며, 노드 간에는 부모-자식 관계가 존재한다. 트리를 이해하기 위해 자주 등장하는 용어들을 정리하면 다음과 같다.
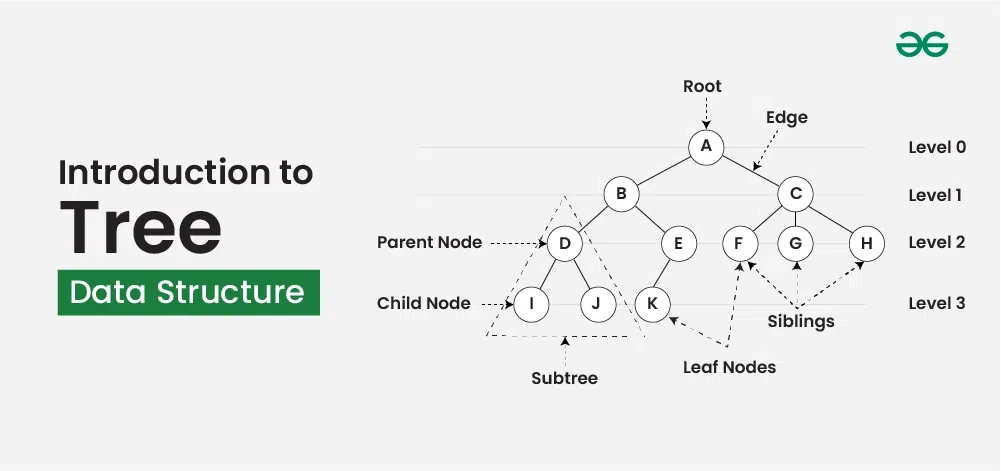
- 루트(Root): 트리의 최상단 노드. 부모가 없으며 트리 전체의 시작점이다.
- 노드(Node): 데이터를 담고 있는 요소로, 루트, 내부 노드, 리프 노드로 나뉜다.
- 간선(Edge): 노드와 노드를 연결하는 선. 하나의 간선은 부모와 자식 노드 간의 관계를 나타낸다.
- 부모(Parent): 한 단계 위에 있는 노드. 자식 노드를 가진다.
- 조상(Ancestor): 기준 노드의 모든 조상
- 자식(Child): 부모로부터 내려온 노드.
- 자손(Descendant): 기준 노드의 모든 후손
- 형제(Sibling): 동일한 부모를 가지는 노드들.
- 사촌(Cousin): 같은 레벨이면서 부모가 다른 노드
- 브랜치(Branch): 자식이 존재하는 노드 (자식이 단 하나라고 해도 브랜치 노드)
- 리프(Leaf): 자식이 없는 노드. 트리의 말단을 구성한다.
- 서브트리(Subtree): 어떤 노드를 루트로 하는 하위 트리.
- 깊이(Depth): 루트에서 특정 노드까지 가는데 필요한 엣지의 수
- 레벨(Level): 같은 깊이를 가진 노드의 그룹 (일반적으로 깊이에서 +1을 함)
- 높이(Height): 가장 깊은 리프 노드까지의 최대 높이 혹은 레
- 차수(Degree): 하나의 노드가 가지고 있는 자식의 수.
트리는 이러한 용어들을 통해 구조를 파악하고, 다양한 형태의 구현이나 탐색에서 기준점을 설정할 수 있다.
트리 구현 방식 : LCRS vs N - Link
트리는 메모리 구조상 배열보다는 연결 구조로 구현되는 경우가 많다. 이때 사용하는 대표적인 방식이 N-Link 방식과 LCRS(Left-Child Right-Sibling) 방식이다. 각각의 특징은 다음과 같다.
1. N - Link 방식
N-Link는 하나의 노드가 자식 노드의 수만큼 포인터(링크)를 가지고 있는 방식이다. 일반적인 트리 구조에 가장 직관적으로 대응되며, 각 노드는 자식 수에 따라 유동적인 배열 또는 리스트를 가진다.
- 구조: ⟨⟨List<Node> children⟩⟩ 형태
- 장점: 계층 구조 표현이 직관적이며 가독성이 좋다.
- 단점: 자식 수에 따라 노드 크기가 달라지고, 트리 전체의 메모리 사용량이 커질 수 있다.
2. LCRS 방식 (좌-자식 우-형제)
LCRS는 모든 노드가 두 개의 포인터만 가진다. 하나는 왼쪽 자식(Left Child), 하나는 오른쪽 형제(Right Sibling)을 가리킨다. 트리 구조를 이진 트리처럼 표현하는 방식으로, 모든 일반 트리를 이진 트리 형태로 변환할 수 있다는 특성을 이용한다.
- 구조:
class Node { Node leftChild; // 첫 번째 자식 Node rightSibling; // 다음 형제 } - 장점: 노드 구조가 고정되어 공간 낭비가 없다. / 이진 트리의 알고리즘을 사용할 수 있
- 단점: 자식 노드를 순차적으로 접근해야 하며, 코드 복잡도가 높아질 수 있다.
이진 트리
이진 트리는 트리 구조 중 가장 널리 사용되는 형태로, 모든 노드가 최대 두 개의 자식 노드(왼쪽과 오른쪽)를 가지는 구조다. 단순하면서도 다양한 알고리즘의 기반이 되는 만큼, 그 정의와 분류를 정확히 이해하는 것이 중요하다.
이진 트리의 기본 구조
이진 트리는 다음과 같은 특징을 가진다:
- 각 노드는 왼쪽 자식(left child), 오른쪽 자식(right child)을 가질 수 있다.
- 자식이 없는 노드는 리프(leaf)로 간주된다.
- 이진 트리는 재귀적으로 정의될 수 있으며, 이는 다양한 순회 알고리즘 구현에도 유리하게 작용한다.
이진 트리의 주요 종류
이진 트리는 특정 조건을 기준으로 다양한 이름으로 분류된다. 아래는 그 주요한 분류 기준이다:
| 분류 | 설명 |
| 정 이진 트리 (Full Binary Tree) | 모든 노드가 0개 또는 2개의 자식을 가짐 |
| 포화 이진 트리 (Perfect Binary Tree) | 모든 리프 노드가 같은 레벨에 있고, 내부 노드는 모두 자식 2개 |
| 완전 이진 트리 (Complete Binary Tree) | 마지막 레벨을 제외한 모든 레벨이 가득 차 있으며, 마지막은 왼쪽부터 채움 |
| 균형 이진 트리 (Balanced Binary Tree) | 모든 노드의 왼쪽과 오른쪽 서브트리 높이 차이가 일정 범위 이하 |
| 이진 탐색 트리 (Binary Search Tree, BST) | 왼쪽 자식 < 부모 ≤ 오른쪽 자식 규칙을 따르는 정렬 트리 |
| 힙 (Heap) | 완전 이진 트리 기반, 부모가 자식보다 크거나 작음 (최대/최소 힙) |
이진 트리 구현 방식 비교 : List vs Node
이진 트리는 크게 두 가지 방식으로 구현할 수 있다. 하나는 배열(List) 기반, 다른 하나는 연결 노드(Node) 기반이다. 두 방식은 트리의 용도나 상황에 따라 장단점이 분명하므로, 구현 목적에 따라 선택해야 한다.
1. 배열(List) 기반 구현
이 방식은 완전 이진 트리를 기반으로 한다. 노드를 배열의 인덱스로 표현하며, 부모-자식 간의 관계를 수학적으로 정의할 수 있다.
- 구조 예시:
Index: 0 1 2 3 4 5 6 값: A B C D E F G- 부모(i)의 왼쪽 자식: 2i + 1
- 부모(i)의 오른쪽 자식: 2i + 2
- 자식(i)의 부모: (i - 1) / 2
- 장점:
- 인덱스로 즉시 접근 가능 → 속도가 빠름
- 완전 이진 트리에 매우 적합
- 단점:
- 트리가 희소(sparse)하거나 불균형한 경우 공간 낭비가 큼
- 동적 삽입/삭제 시 구조 변경이 어렵다
2. 노드(Node) 기반 구현
각 노드는 객체로 구성되며, ⟨⟨left⟩⟩와 ⟨⟨right⟩⟩ 포인터를 사용해 자식을 가리킨다.
class TreeNode {
int value;
TreeNode left;
TreeNode right;
}- 장점:
- 불균형 트리나 비정형 구조에서도 유연하게 적용 가능
- 삽입/삭제가 자연스럽고 확장성 있음
- 단점:
- 노드 간 접근은 순회(traversal)가 필요
- 메모리 접근 비용이 높고, 구현이 복잡할 수 있음
3. 비교 요약
| 기준 | 배열(List) 방식 | 노드(Node) 방식 |
| 구조 적합도 | 완전 이진 트리에 적합 | 모든 형태의 트리에 적합 |
| 메모리 효율 | 희소 트리에선 비효율적 | 노드 수만큼만 메모리 사용 |
| 구현 복잡도 | 간단 | 복잡 |
| 삽입/삭제 | 어려움 | 상대적으로 쉬움 |
| 접근 방식 | 인덱스로 바로 접근 | 순회 필요 |
힙처럼 완전 이진 트리 기반 구조는 배열로, 검색 트리나 동적 트리는 노드 기반으로 구현하는 것이 일반적이다.
'Java > 알고리즘(코테)' 카테고리의 다른 글
| BFS (너비 우선 탐색, Breadth-First Search) (0) | 2025.05.16 |
|---|---|
| DFS (깊이 우선 탐색, Depth-First Search) (1) | 2025.05.15 |
| Graph (그래프) (0) | 2025.05.12 |
| 자료구조 알고리즘 목차 (0) | 2025.05.11 |
| Quick Sort (퀵 정렬) (0) | 2025.05.11 |


